
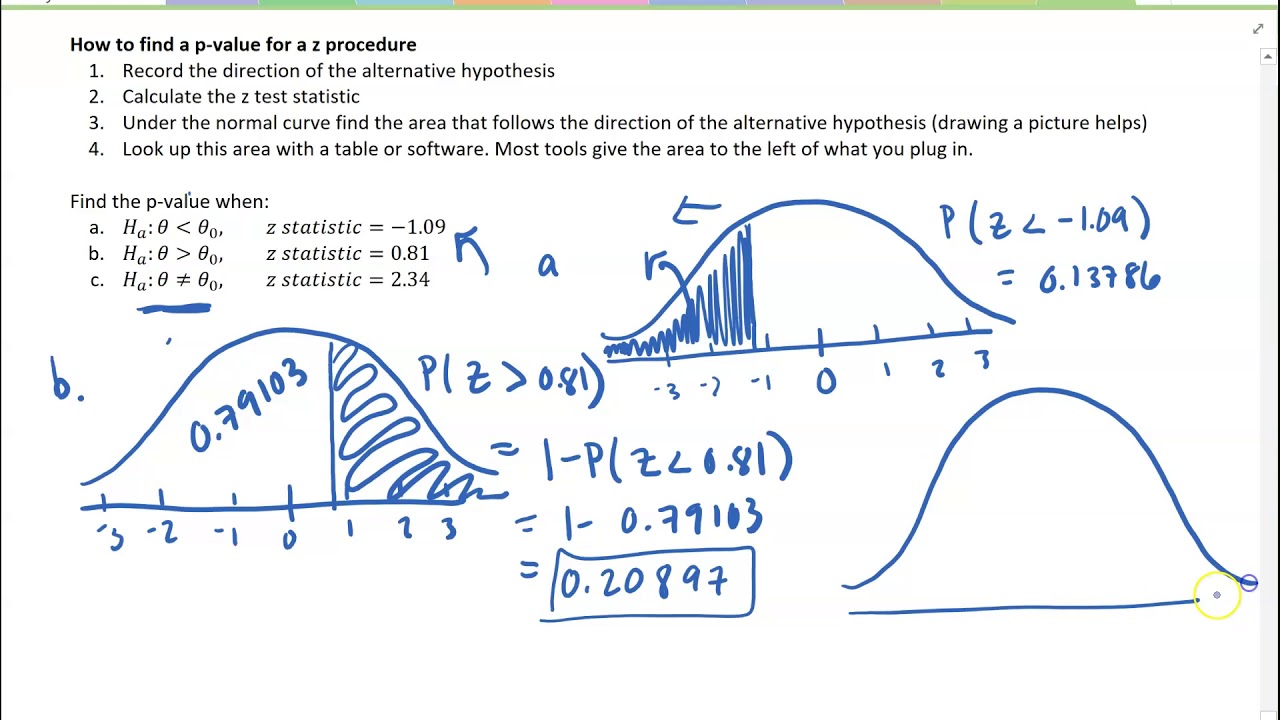
So the null hypothesis is kept at all of these significance levels. Here is an illustration of this test in a graph: This P-value is bigger than any of the common significance levels (10, 5, 1). The normal distribution table for left-tailed test is given below. This tells us that the significance level ((alpha)) would need to be smaller 0.3996, or 39.96, to reject the null hypothesis. The normal distribution table for right-tailed test is given below. The t table for two tail probability is given below. In this case, the t critical value is 2.132. Pick the value occurring on the intersection of mentioned row and column. Also look for the significance level α in the top row. Look for the degree of freedom in the most left column. Subtract 1 from the sample size to get the degree of freedom.ĭepending on the test, choose one tailed t distribution table or two tailed t table below. However, if you want to find critical values without using t table calculator, follow the examples given below.įind the t critical value if size of the sample is 5 and significance level is 0.05. The t distribution table (student t test distribution) consists of hundreds of values, so, it is convenient to use t table value calculator above for critical values.

U is the quantile function of the normal distribution,Ĭritical value of t calculator uses all these formulas to produce exact critical values needed to accept or reject a hypothesis.Ĭalculating critical value is a tiring task because it involves looking for values into t distribution chart. Q t is the quantile function of t student distribution,


 0 kommentar(er)
0 kommentar(er)
